Problem Solving Strategies

When encountering a novel problem, a person will attempt to solve it by carrying out certain actions. The person may first conceive several possible solutions mentally based on gathered information and existing knowledge. These potential solutions are then whittled down to a few viable solutions, using some kind of decision-making process to weigh the cost or compare the outcome against the odds.
In the end, the person may choose to attempt ‘solving the problem’ by performing certain actions, or avoid the problem altogether if the costs or odds are too high. Take the Gordian Knot, for example, Alexander the Great decided to overcome the “unsolvable problem” by slicing the knot in two — thereby, circumventing it. In other words, Alexander the Great made a conscious decision to ‘not’ play by the rule (after considering his options).
Additional knowledge can help the person (1) arrive at a better potential solution, (2) pick a solution if the solution already exists. Sometimes, the newly encountered problem may match an existing pattern. In that case, the person may evaluate relevant solutions to see if an existing one can be modified to solve the problem in the current situation.
Expert Decisions
Psychology research showed experts to have very different problem-solving strategies compared to novices. In chess playing, it has been found that Master chess players stored large collections of chess formations in memory and were able to quickly reproduce the right move when presented with a familiar formation. Besides having a large domain-specific knowledge, experts also differ from novices in the strategies of problem-solving, the way they search for information (gaze patterns), the speed and accuracy of muscular movement execution, etc.
As learning is an internal cognitive event occurring within the brain, it cannot be directly measured or observed. What can be measured is the observable actions performed after the decision has been made to solve a problem. Although decision-making can be analyzed using a qualitative or quantitative approach, the quantitative method is especially useful to the training industry because:
- it is empirical — based on data, information, logic,
- it is scalable — generalizable to bigger populations,
- it has predicting power — can be used to model and predict other similar scenarios at the absence of better data, and
- it can be used to effectively justify the decision chosen (and for the calculation of the return of investment).
Researchers are able to calculate the value of decision outcome using statistical Decision Theory analysis. The framework allows researchers to assess and determine if a decision made is optimal under certain conditions, e.g., certainty, uncertainty, or at risk.
Strategy Before Speed
Researchers can draw from a number of decision analysis techniques to evaluate whether a decision (made under certain conditions) is optimal. Techniques such as these are necessary for the calculation of the values of the outcome — usually expressed as a value or an index. There are several factors that can be used to judge whether a decision is good or not, “cost” being the most common. When dealing with the issue of cost, it can be taken to mean time or resources. When making a decision, a person must:
- identify and define the problems,
- identify possible solutions and alternatives,
- evaluate each possible alternatives, and
- select the best/optimal alternatives within a certain time constraint.
Simply choosing a good plan of action is not good enough. Because “time is money,” the decision must be made within certain time constraints so as not to incur further cost. Conversely, speed/time alone is not the sole criterion for good decision-making (despite it being the case in many entertainment games). A good plan of action (i.e., strategy) must be complemented with time or speed of completion: surgery, being the case in point.
Being able to perform well under time pressure is a hallmark of expertise because many people do not perform well under time pressure. Research has shown that people may take the unnecessary risk under (time) pressure. Therefore, the best training approach is to implement strategies before speed and the approach is consistent with the Skill Acquisition Models.
![]()
Expert’s Solution as the Critical Path
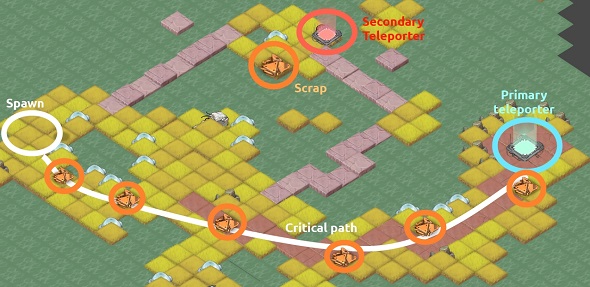
There are two ways of calculating the value of decisions. The first approach is statistical decision analysis methods that use (scientific) analysis method to arrive at the optimal decision independent of expert’s input. In fact, the decision arrived through such a method may be completely different from that made by the experts. Examples are:
- Decision Tree — a technique that can be used to represent and visualize the decisions made by learners.
- Artificial Neural Network (ANN) — a technique that can be used to determine the optimal solution based on observations and the cost associated with the alternatives.
Instead of determining the optimal path mathematically independent of experts’ input, the second approach assumes the experts’ paths to be the best ways to solving the problem. Example include:
- Information Trails — an assessment method designed for virtual environment training that uses known experts’ performance as the baseline of evaluation.
Information Trails is unique because it places the learners on an Expertise continuum based on their Expertise Index score. Given the user data, the approach makes use of data mining and statistical learning methods to classify learners into likely-experts or novices categories and predict what kinds of decisions are most likely to occur and be made by whom: experts or novices. This approach is consistent with the critical path in game design [4].
![]()
References:
- Loh, C. S. & I-Hung, Li. (Sep 2015). Predicting the Competency Improvement for Serious Games Analytics: Action-sequences, Game Grids, PLS-DA and JMP. Proceedings of the Discovery Summit 2015. San Diego, CA. [LINK] [PDF] DOI: 10.13140/RG.2.1.3997.4889
- Loh, C. S., & Sheng, Y. (2014). Maximum Similarity Index (MSI): A metric to differentiate the performance of novices vs. multiple-experts in serious games. Computers in Human Behavior. 39: 322-330. DOI: 10.1016/j.chb.2014.07.022
- Loh, C. S. & Sheng, Y. (July 2013). Performance metrics for serious games: Will the (real) expert please step forward? Proceedings of the 18th International Conference on Computer Games: AI, Animation, Mobile, Interactive Multimedia, Educational & Serious Games (CGAMES 2013). Louisville, KY. [PDF] DOI:10.1109/CGames.2013.6632633
- Critical Path: https://www.gamedeveloper.com/design/level-design-in-procedural-generation